La geometria del carbonio e di qualche suo composto
Il carbonio è l’elemento che più si presta ad una trattazione semplificata. I risultati che seguono sono basati su considerazioni qualitative e ripropongono la tematica della Molecular Geometry (si veda la nota a fine pagina), finalizzata essenzialmente nella determinazione della distribuzione di nuclei ed elettroni dove ciò sia ritenuto tecnicamente più ragionevole, e non con considerazioni puramente probabilistiche come suggerito dalla meccanica quantistica. Il sottofondo elettromagnetico, sollecitato dall’azione dei nuclei, si organizza in strutture localizzate che rispettano le equazioni dell’elettrodinamica. In esse, l’informazione viene trasportata a velocità comparabili a quella della luce. Il calcolo esplicito di queste dinamiche è tutt’altro che banale, per cui non entriamo qui nei dettagli. Le strutture possono avere qualche affinità con i cosiddetti ‘orbitali’. Di fatto, la loro geometria può essere determinata attraverso il calcolo delle autofunzioni di un opportuno problema di tipo ellittico, similmente a quanto viene fatto nel caso dell’equazione di Schrodinger. Tuttavia il significato è totalmente differente. Il classico orbitale suggerisce la distribuzione di probabilità di trovare elettroni ‘orbitanti’, che seguono la scia di un’astratta funzione d’onda. Nel nostro caso, le geometrie delimitano l’evoluzione di campi elettromagnetici concreti e non sono in relazione con gli elettroni, che prendono invece posto, in un secondo tempo, in specifiche locazioni dettate delle circostanze.
The geometry of carbon and some of its compounds
Carbon is the element that best lends itself to a simplified treatment. The following results are based on qualitative considerations and replicate the theme of Molecular Geometry (see the note at the end of the page), essentially finalized in the determination of the distribution of nuclei and electrons where this is deemed technically more reasonable, and not with purely probabilistic considerations as suggested by quantum mechanics. The electromagnetic background, solicited by the action of the nuclei, organizes itself in localized structures respecting the equations of electrodynamics. Inside them, information is transported at speeds comparable to that of light. The explicit calculation of these dynamics is far from trivial, so we will not discuss any details here. These structures may have some affinity with the so-called ‘orbitals”. In fact, their geometry can be determined by calculating the eigenfunctions of an appropriate problem of elliptic type, similarly to what is done in the case of the Schrodinger equation. However, the meaning is totally different. The classic orbital suggests the probability distribution for finding ‘orbiting’ electrons, following the trail of an abstract wavefunction. In our case, the geometries delimit the evolution of effective electromagnetic fields and are not related with the electrons, which instead take their place, at a later time, in specific locations dictated by the circumstances.
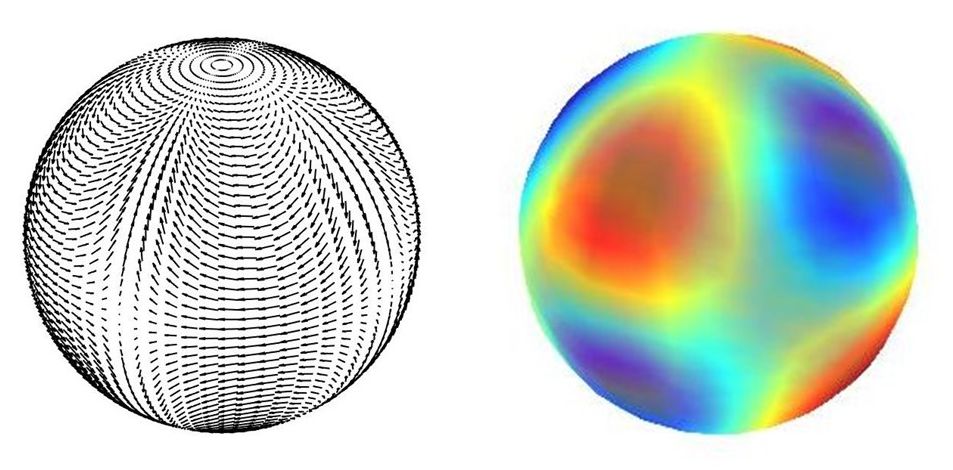
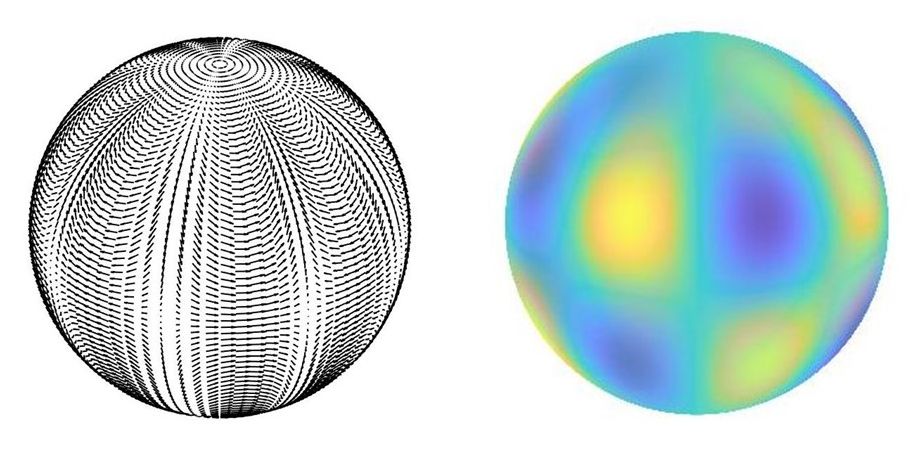
Per il carbonio ipotizziamo la situazione seguente. Tra le tante autofunzioni vettoriali, quella in figura corrisponde all’orbitale f_xyz, con la differenza fondamentale che viene invece rappresentato l’andamento del campo magnetico ad una certa distanza dal nucleo. Tale campo diventa uniformemente nullo sulla superficie sferica corrispondente ad un raggio ben definito (che qui non stiamo a specificare, ma tuttavia compatibile con le distanze internucleari). Su quest’ultima superficie si depositeranno i quattro elettroni di valenza. Gli altri due elettroni si trovano sulla superficie di una sferetta interna (non visualizzata) avente una distribuzione del campo magnetico che ricorda quella dell’orbitale p_z. In realtà tutti i campi coinvolti sono in continua evoluzione in accordo con i classici modelli dell’elettromagnetismo. Pertanto anche un complicato campo elettrico è presente e permea tutta la struttura. Questo si somma a quello stazionario del nucleo. In figura appaiono quindi otto vortici magnetici (4 destrorsi e 4 sinistrorsi), indicati da diversi colori. Ricordiamo ancora una volta che qui la trattazione è molto qualitativa, anche se dei calcoli effettivi potrebbero essere svolti.
For carbon we assume the following situation. Among the many vector eigenfunctions, the one in the figure corresponds to the orbital f_xyz, with the key difference that the displacement of the magnetic field at some distance from the nucleus is instead represented. Such a field becomes uniformly zero on the spherical surface corresponding to a well-defined radius (which we are not going to specify here, but nevertheless compatible with the internuclear distances). The four valence electrons will lie on this last surface. The other two electrons will be on the surface of an inner sphere (not shown) having a distribution of the magnetic field which resembles that of the p_z orbital. Actually, all fields involved are constantly evolving in accordance with the classical models of electromagnetism. Therefore, also a complex electric field is present and permeates the whole structure. This adds up to the stationary one of the nucleus. Eight magnetic vortices therefore appear in the figure (4 right-handed and 4 left-handed), indicated by different colors. We recall once again that the discussion here is very qualitative, although actual calculations could be performed.
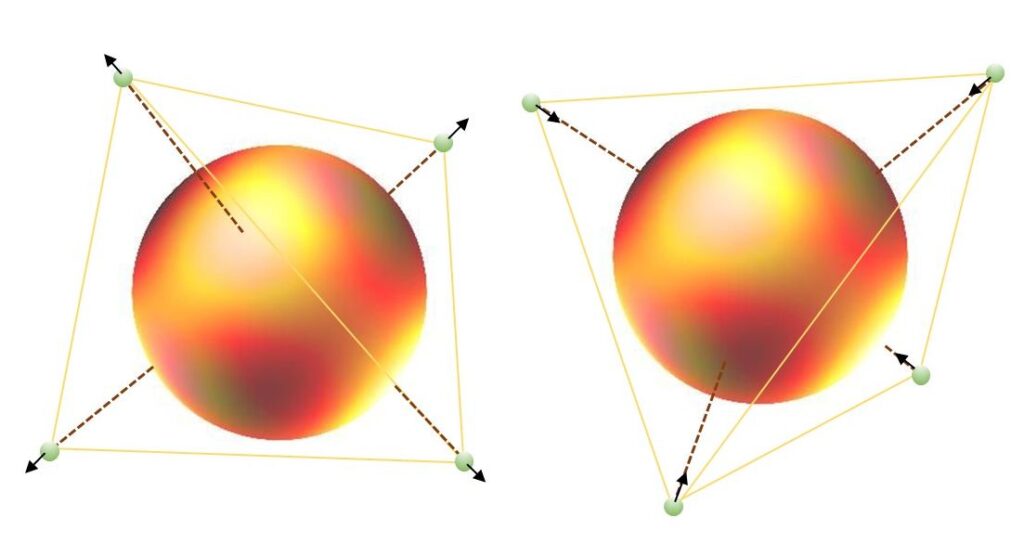
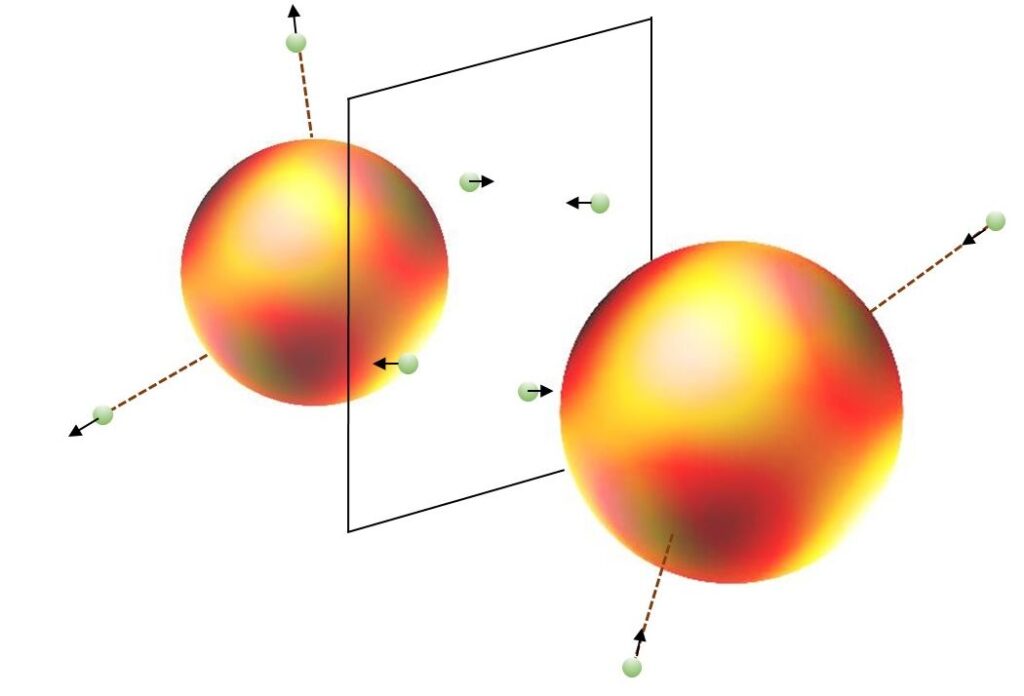
L’atomo di carbonio risulta essere composto dai seguenti ingredienti: un nucleo, una palla elettromagnetica in continuo fermento e del diametro dell’ordine dell’Angstrom, sei elettroni opportunamente localizzati (non necessariamente rotanti, ma fluttuanti attorno a posizioni di equilibrio). Due elettroni sono vicini al nucleo e presentano spin opposti, gli altri quattro si distribuiscono ai vertici di un tetraedro. Come si osserva nella figura seguente, proponiamo per essi due possibili distribuzioni (da ritenersi in pratica equivalenti). In entrambi i casi, la risultante dei vettori di spin è nulla. I pallini verdi sono piccoli anelli, come QUI ipotizzato, dove il vettore di spin è orientato ortogonalmente al campo magnetico. Sollecitando un elettrone si ottengono delle fluttuazioni locali del sottofondo elettromagnetico, che possono concretizzarsi in una emissione di fotoni in maniera quantizzata, in accordo con lo spettro atomico. Non è dunque l’accelerazione dell’elettrone dovuta al suo cambiamento di orbita a produrre energia elettromagnetica sotto forma di fotone (meccanismo difficile da spiegare se non in maniera fenomenologica), ma l’espulsione di energia in sovrappiù già presente nell’atomo eccitato. Un calcolo sommario riguardo al caso dell’atomo di idrogeno viene proposto in D. Funaro, From Photons to Atoms – The Electromagnetic Nature of Matter, DOI: 10.1142/11383, Appendice I.
The carbon atom turns out to be composed of the following ingredients: a nucleus, an electromagnetic ball in continuous movement and with a diameter of the order of the Angstrom, six suitably localized electrons (not necessarily rotating, but fluctuating around equilibrium positions). Two electrons are close to the nucleus and exhibit opposite spins, the other four are distributed at the vertices of a tetrahedron. As you observe in the following figure, we propose two possible distributions for them (to be considered equivalent in practice). In both cases, the resultant of the spin vectors is zero. The green dots are small rings, as hypothesized HERE, where the spin vector is oriented orthogonally to the magnetic field. By stimulating an electron, local fluctuations of the electromagnetic background are obtained which can materialize in an emission of photons in a quantized manner, in accordance with the atomic spectrum. It is therefore not the acceleration of the electron due to its change of orbit to produce electromagnetic energy in the form of a photon (a mechanism that is difficult to explain, except in phenomenological manner), but the expulsion of excess energy already present in the excited atom. A qualitative calculation regarding the case of the hydrogen atom is proposed in D. Funaro, From Photons to Atoms – The Electromagnetic Nature of Matter, DOI: 10.1142/11383, Appendix I.
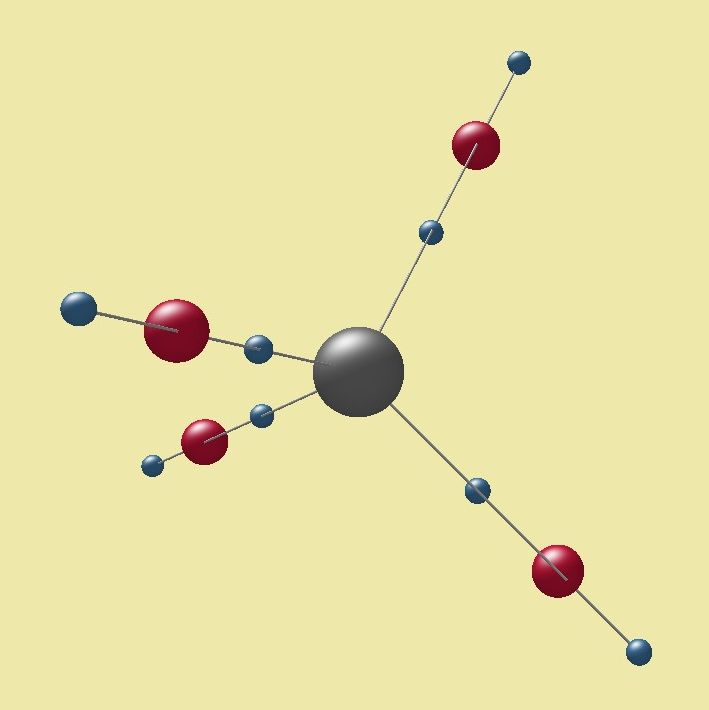
La molecola di metano è presto fatta. Basta aggiungere quattro protoni (palle rosse) e quattro elettroni (palle blu). Si ha quindi un totale di 12 elettroni, considerando anche quelli (non mostrati) che giacciono vicino al nucleo di carbonio (conferendogli una piccola asimmetria). Come in precedenza, i componenti mantengono posizioni stabili. Le reali proporzioni sono dettate non solo dall’equilibrio delle cariche stazionarie, ma dall’azione esercitata da opportune bolle elettromagnetiche. La costituzione di esse caratterizza la molecola più di quanto non facciano le sue componenti. La distruzione della molecola non porta solo al disfacimento dei legami, ma alla ricostituzione del sottofondo secondo diverse geometrie, tanto da suggerire che “il tutto non sia sempre la somma delle parti”.
The methane molecule is soon done. Just add four protons (red balls) and four electrons (blue balls). We therefore have a total of 12 electrons, including those (not shown) that lie close to the carbon nucleus (providing a small asymmetry to the molecule). As before, all components maintain stable positions. The actual proportions are dictated not only from the equilibrium of the stationary charges, but from the action exerted by suitable electromagnetic bubbles. Their constitution characterizes the molecule more than his own components. The destruction of the molecule not only leads to the unraveling of the bonds, but to reconstruction of the background according to different geometries, so as to suggest that “the whole is not always the sum of its parts”.
Discorsi analoghi valgono per l’etilene e l’acetilene (riportati qua sotto). Si noti la differente orientazione dell’autofunzione in modo da simulare un doppio o un triplo legame.
Similar arguments apply to ethylene and acetylene (shown below). Note the different orientation of the eigenfunction so as to simulate a double or triple bond.
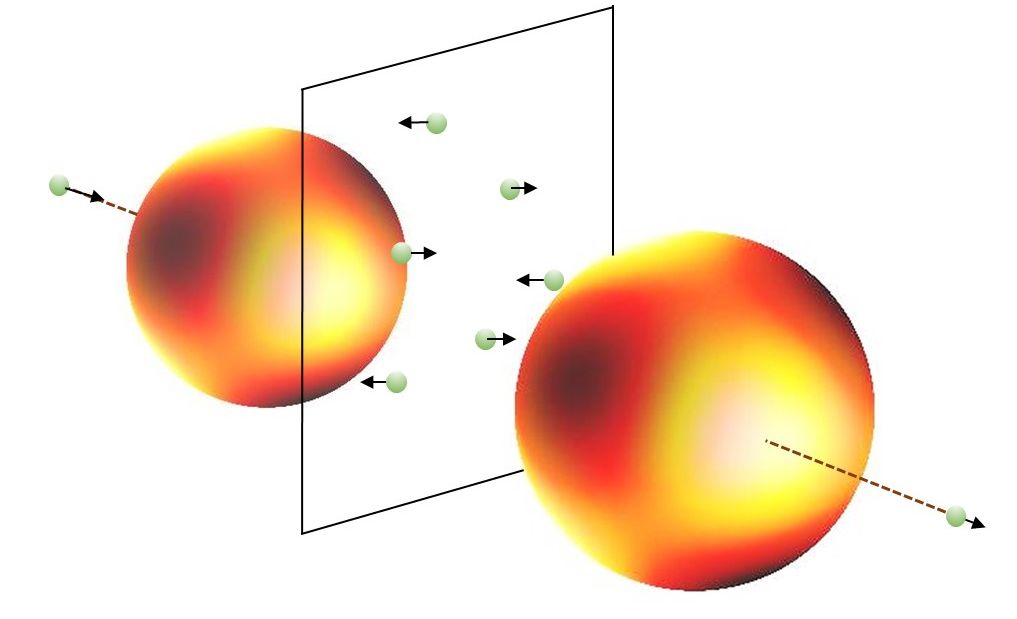
Come ultimo esempio mostriamo come appare la situazione nel caso del benzene. Nella trattazione classica occorre ipotizzare l’esistenza sia di legami singoli che doppi (la casistica del grafene diventa in tal modo assai più variegata). Se si considera invece il posizionamento specifico degli elettroni, il corrispondente diagramma diventa perfettamente simmetrico.
As a last example, we show what the situation looks like in the case of benzene. In the classical treatment it is necessary to assume the existence of both single and double bonds (the taxonomy of graphene thus becomes much more varied). If instead the specific positioning of the electrons is considered, the corresponding diagram becomes perfectly symmetrical.
 |  |
La seguente disposizione si presta molto bene a descrivere il neon (ma anche l’azoto o l’ossigeno). Questa volta ci sono otto vortici destrorsi e otto sinistrorsi. All’interno (non visibile) c’è ancora una sferetta del tipo p_z. Nel caso del neon, oltre ai due più vicini al nucleo, vi sono altri otto elettroni (con spin divergenti o convergenti) fluttuanti a distanza in modo da formare un parallelepipedo. La forte repulsività del nucleo (con carica pari a dieci) non permette a dei protoni di avvicinarsi all’atomo completo (malgrado la presenza degli elettroni esterni), non garantendo quindi la possibilità di creare legami solidi. Nel caso dell’acqua invece, due atomi di idrogeno possono trovare posto in modo da essere più lontani possibile. A causa della conformazione geometrica dell’autofunzione e del principio di esclusione di Pauli, non possono piazzarsi diametralmente opposti, ma sono costretti a formare un angolo ottuso.
The following arrangement lends itself very well to describing neon (but also nitrogen or oxygen). This time, there are eight right-handed and eight left-handed vortices. Inside (not visible), there is still a sphere of the type p_z. In the case of neon, in addition to those close to the nucleus, there are eight other electrons (with either diverging or converging spins) floating at a distance so as to form a parallelepiped. The strong repulsiveness of the nucleus (with a charge equal to ten) does not allow protons to approach the complete atom (despite the presence of external electrons), thus not guaranteeing the possibility of creating solid bonds. In the case of water however, two hydrogen atoms can find a place so as to be as far apart as possible. Due to the geometric conformation of the eigenfunction and Pauli’s exclusion principle, they cannot be placed diametrically opposite but are forced to form an obtuse angle.
With the term Molecular Geometry, we indicate here that branch of chemistry that underlines the geometrical aspects of compounds on the basis of arguments mainly devoted to the minimization of functionals related to electrostatic energy. The basic ideas developed in the 1950s and today’s version is the contribution of several authors. We limit ourselves here to quoting the following text, where the fundamental lines of the theory are exposed:
R.J. Gillespie, P.L.A. Popelier, Chemical Bonding and Molecular Geometry – From Lewis to Electron Densities, Oxford University Press, New York (2001).
We also report the following sentence from the introduction: Although this model can be regarded as an empirical model that does not directly use quantum mechanical ideas, its physical basis is to be found in the Pauli principle.
The work we are describing here in these pages has many similarities with the approach just introduced. For example, the scheme of methane is the same reported in Gillespie-Popelier on page 31. Although not thoroughly explored, the considerations made here may be of help in providing further ideas and theoretical support. But above all they serve us to stress that a geometric organization of the electromagnetic background is in line with other research topics. In this new version the role of the stationary electric field remains important but not essential, while the dynamics of the electromagnetic fields is the engine that forms and holds the molecule together.